삼각함수

$r=\sqrt{x^2}+{y^2}$
| $𝜽$ | $0°$ | $30°$ | $45°$ | $60°$ | $90°$ |
| $sin𝜽$ | $0$ | $\frac{1}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{\sqrt{3}}{2}$ | $1$ |
| $cos𝜽$ | $1$ | $\frac{\sqrt{3}}{2}$ | $\frac{\sqrt{2}}{2}$ | $\frac{1}{2}$ | $0$ |
| $tan𝜽$ | $0$ | $\frac{\sqrt{3}}{3}$ | $1$ | $\sqrt{3}$ | X |
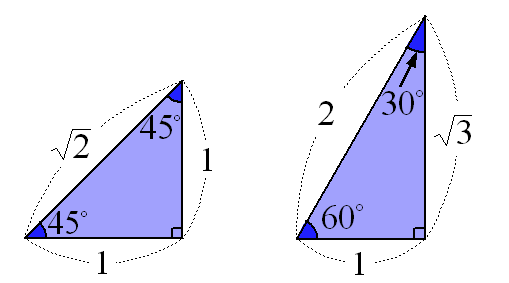
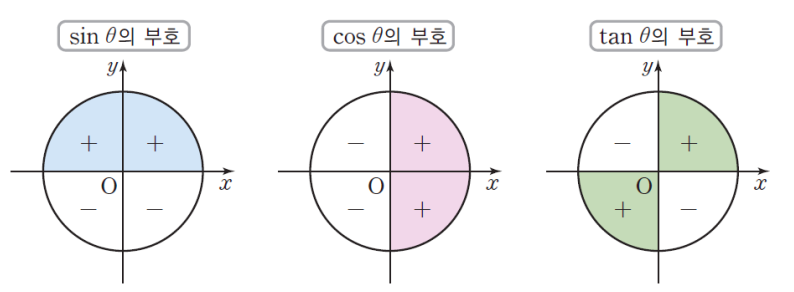
삼각함수 사이의 관계
$tan𝜽=\frac{sin𝜽}{cos𝜽}$
$sin^{2}𝜽+cos^{2}𝜽=1$
삼각함수의 그래프
| $y=\sin x$ | $y=\cos x$ | $y=\tan x$ | |
| 그래프 | 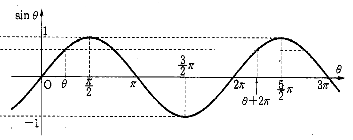 |
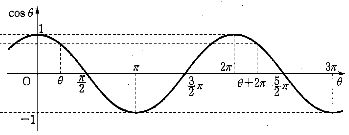 |
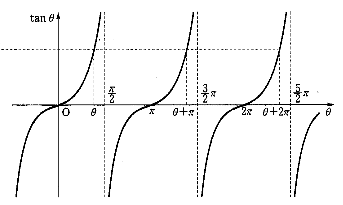 |
| 정의역 | 실수 전체의 집합 | 실수 전체의 집합 | $y=n\pi+\frac{\pi}{2}$(n은 정수) 를 제외한 실수 전체의 집합 |
| 치역 | $\{y|-1≤y≤1\}$ | $\{y|-1≤y≤1\}$ | 실수 전체의 집합 |
| 주기 | $2\pi$ | $2\pi$ | $\pi$ |
| 대칭성 | 원점에 대하여 대칭 | $y$축에 대하여 대칭 | 원점에 대하여 대칭 |

| 함수 $y=$$a$$\sin{x}$ | 함수 $y=$$a$$\cos{x}$ | 함수 $y=$$a$$\tan{x}$ | |
| 치역 | $\{y| -|$$a$$|≤y≤|$$a$$|\}$ | $\{y| -|$$a$$|≤y≤|$$a$$|\}$ | 모든 실수 |
| 함수 $y=\sin$$b$$x$ | 함수 $y=\cos$$b$$x$ | 함수 $y=\tan$$b$$x$ | |
| 주기 | $\{\frac{2\pi}{|\textcolor{red}{b}|}\}$ | $\{\frac{2\pi}{|\textcolor{red}{b}|}\}$ | $\{\frac{\pi}{|\textcolor{red}{b}|}\}$ |
삼각함수의 성질
- $\sin(\pi+x)=-\sin x$
- $\sin(\frac{\pi}{2}+x)=-\cos x$
- $\cos(\pi+x)=-\cos x$
- $\cos(\frac{\pi}{2}+x)=-\sin x$
- $\tan(\pi+x)=\tan x$
- $\tan(\frac{\pi}{2}+x)=-\frac{1}{\tan x}$
사인법칙
- 사인법칙: 삼각형 $ABC$에서 $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$
- 코사인법칙: 삼각형 $ABC$에서
- $a^2=b^2+c^2-2bc \cos A$
- $b^2=c^2+a^2-2ca \cos B$
- $c^2=a^2+b^2-2ab \cos C$
- 삼각형의 넓이: 삼각형 $ABC$의 넓이를 $S$라 하면
- $S$
$=\frac{1}{2}ab \sin C$
$=\frac{1}{2}bc \sin A$
$=\frac{1}{2}ca \sin B$
- $S$
수열
| 수열 | 차례로 늘어놓은 수의 열 |
| 항 | 수열을 이루고 있는 각각의 수 |
| 일반항 | 제 $n$항 $a_n$ ($\{a_n\}$) |
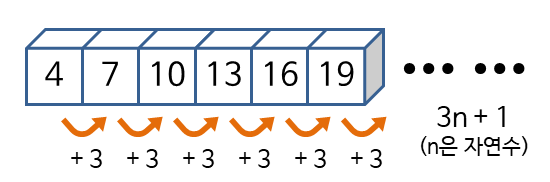
| 등차수열 | 첫째항에 차례로 일정한 수를 더하여 만든 수열 |
| 공차 | 더하는 일정한 수 |
| 등차수열의 일반항 | 첫째항이 $a$, 공차인 $d$인 등차수열 ${a_n}$의 일반항은 $a_n=a+(n-1)d$ $(n=1, 2, 3, ⋯)$ |
| 등차중항 | 세 수 $a, b, c$가 이 순서대로 등차수열을 이룰 때 $b$ 이때 $b-a=c-b$이므로 $b=\frac{a+c}{2}$ |
| 등차수열의 합 | 등차수열의 첫째항부터 제$n$항까지의 합 $S_n$은 1. 첫째항이 $a$, 제$n$항이 $l$일 때 $S_n=\frac{n(a+l)}{2}$ 2. 첫째항이 $a$, 공차가 $d$일 때 $S_n=\frac{n\{2a+(n-1)d\}}{2}$ |
| 수열의 합과 일반항 사이의 관계 | 수열 $\{a_n\}$의 첫째항부터 제$n$항까지의 합을 $S_n$이라 하면 $a_1=S_1$, $a_n=S_n-S_{n-1}$ (n≥2) |
| 등비수열 | 첫째항에 차례로 일정한 수를 곱하여 만든 수열 |
| 공비 | 곱하는 일정한 수 |
| 등비수열의 일반항 | 첫째항이 $a$, 공비가 $r(r≠0)$인 등비수열 ${a_n}$의 일반항은 $a_n=ar^{n-1}$ $(n=1, 2, 3, ⋯)$ |
| 등비중항 | 0이 아닌 세 수 $a, b, c$가 이 순서대로 등비수열을 이룰 때 $b$ 이때 $\frac{b}{a}=\frac{c}{b}$이므로 $b^2=ac$ |
| 등비수열의 합 | 첫째항이 $a$, 공비가 $r(r≠0)$인 등비수열의 첫째항부터 제$n$항까지의 합 $S_n$은 1. r≠1일 때 $S_n=\frac{a(1-r^n)}{1-r}=\frac{a(r^n-1)}{r-1}$ 2. r=1일 때 $S_n=na$ |
| 시그마 $\sum\limits_{k=1}^n a_k$ | 수열 $\{a_n\}$의 첫째항부터 제$n$항까지의 합 |
| 합의 기호 $\sum$의 성질 | 1. $\sum\limits_{k=1}^n (a_k+b_k)=\sum\limits_{k=1}^n a_k + \sum\limits_{k=1}^n b_k$ 2. $\sum\limits_{k=1}^n (a_k-b_k)=\sum\limits_{k=1}^n a_k-\sum\limits_{k=1}^n b_k$ 3. $\sum\limits_{k=1}^n ca_k=c\sum\limits_{k=1}^n a_k$ (단, $c$는 상수) 4. $\sum\limits_{k=1}^n c=cn$ (단, $c$는 상수) |
| 자연수의 거듭제곱의 합 | 1. $1+2+3+⋯+n=\sum\limits_{k=1}^n k=\frac{n(n+1)}{2}$ 2. $1^2+2^2+3^2+⋯+n^2=\sum\limits_{k=1}^n k^2=\frac{n(n+1)(2n+1)}{6}$ 3. $1^3+2^3+3^3+⋯+n^3=\sum\limits_{k=1}^n k^3=\{\frac{n(n+1)}{2}\}^2$ |
'----------고2---------- > 수학' 카테고리의 다른 글
| [고2 수학] 1학기 2차 연습 문제 (0) | 2024.06.19 |
|---|---|
| [고2 수학] 1학기 1차 연습 문제 (2) | 2024.04.20 |
| [고2 수학] 1학기 1차 지필평가 (0) | 2024.03.17 |
