지수가 자연수일 때의 지수법칙
$a,\,b$가 실수이고 $m,\,n$이 자연수일 때
- $a^{m}a^{n}=a^{m+n}$
- $(a^{m})^{n}=a^{mn}$
- $(ab)^{n}=a^{n}b^{n}$
- $(\frac{a}{b})^{n}=\frac{a^{n}}{b^{n}}\,(단,\,b≠0)$
- $a^{m}÷a^{n}=\begin{cases}a^{m-n}\;\,(m>n)\\\quad1\;\quad(m=n)\,(단,\,a≠0)\\\frac{1}{a^{n-m}}\quad(m<n)\end{cases}$
더보기
- $2^{4}×2^{5}=2^{4+5}=2^{9}$
- $(2^{4})^{5}=2^{4×5}=2^{20}$
- $(2×3)^{5}=2^{5}×3^{5}$
- $(\frac{2}{3})^{5}=\frac{2^{5}}{3^{5}}$
- $2^{4}÷2^{5}=\frac{1}{2^{5-4}}=\frac{1}{2}$
지수함수
거듭제곱의 성질
$a>0,\,b>0$이고 $m,\,n$이 $2$ 이상의 정수일 때
- $\sqrt[n]{a}\sqrt[n]{b}=\sqrt[n]{ab}$
- $\frac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\frac{a}{b}}$
- $(\sqrt[n]{a})^{m}=\sqrt[n]{a^{m}}$
- $\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}$
더보기
- $\sqrt[5]{2}×\sqrt[5]{3}=\sqrt[5]{2×3}$
- $\frac{\sqrt[5]{2}}{\sqrt[5]{3}}=\sqrt[5]{\frac{2}{3}}$
- $(\sqrt[5]{2})^{4}=\sqrt[5]{2^{4}}=\sqrt{2^{\frac{4}{5}}}$
- $\sqrt[4]{\sqrt[5]{2}}=\sqrt[4×5]{2}=\sqrt[20]{2}$
0 또는 음의 정수인 지수
$a≠0$이고 $n$이 양의 정수일 때
- $a^{0}=1$
- $a^{-n}=\frac{1}{a^{n}}$
더보기
- $2^{0}=1$
- $2^{-3}=\frac{1}{2^{3}}$
유리수인 지수
$a>0$이고 $m,\,n\,(n≥2)$이 정수일 때
- $a^\frac{m}{n}=\sqrt[n]{a^{m}}$
- $a^\frac{1}{n}=\sqrt[n]{a}$
더보기
- $2^\frac{3}{4}=\sqrt[3]{2^{4}}$
- $2^\frac{1}{4}=\sqrt[4]{2}$
로그함수
로그의 정의
$a>0,\,a≠1,\,N>0$일 때
$\qquad a^x=N\,\Longleftrightarrow\,x=log_a{N}$
더보기
$\qquad 2^4=16\,\Longleftrightarrow\,4=log_2{16}$
로그의 밑의 변환
$a>0, a≠1, b>0, c>0, c≠1$일 때
$\qquad log_a{b}=\frac{log_c{b}}{log_c{a}}$
더보기
$\qquad log_4{8}=\frac{log_2{8}}{log_2{4}}=\frac{3log_2{2^3}}{2log_2{2^2}}=\frac{3}{2}$
상용로그 (log N)
10을 밑으로 하는 로그
$\log{1000}=log_{10}{10^3}$
$\qquad=3log_{10}{10}$
$\qquad=3$
지수함수
실수 전체의 집합을 정의역으로 하는 함수
$y=(\frac{1}{2})^x$
$y=\pi^x$

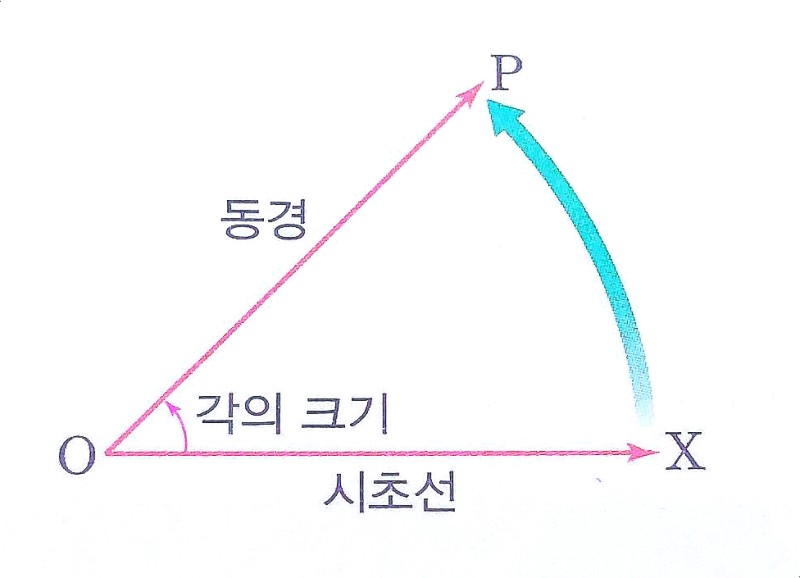
호도법
1라디안$=\frac{180°}{\pi}$
$1°=\frac{\pi}{180}라디안$
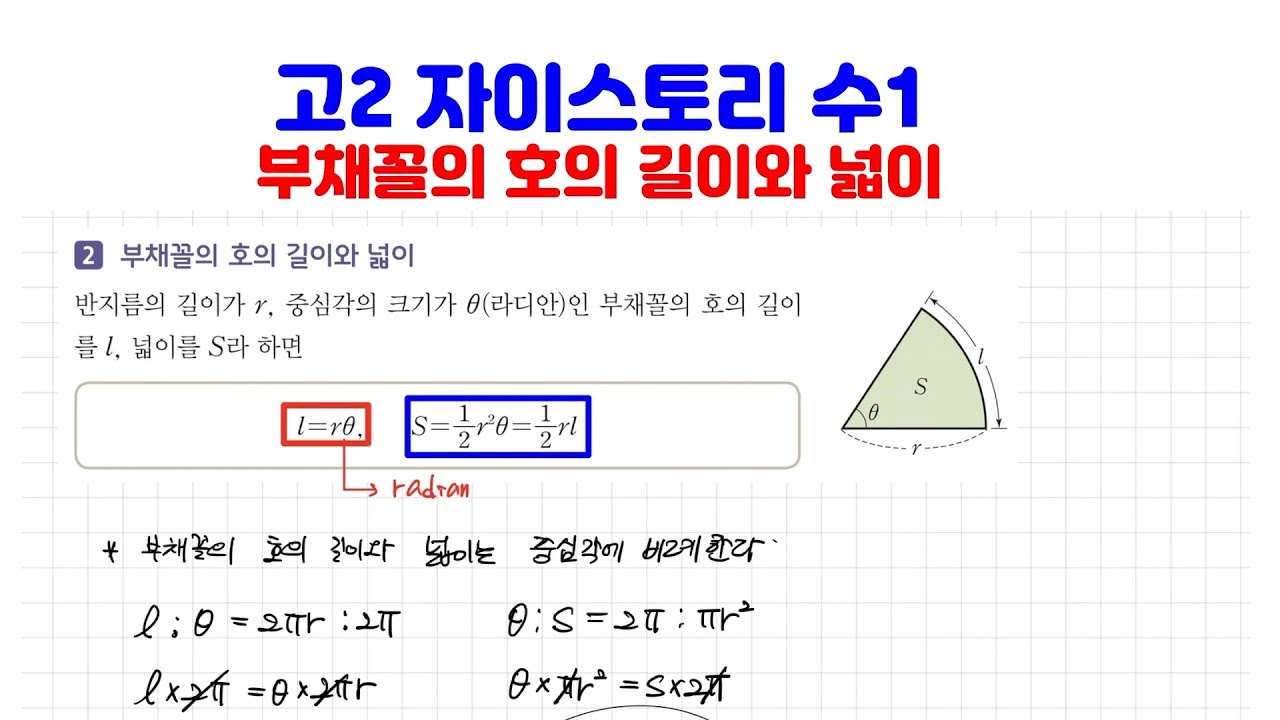
'----------고2---------- > 수학' 카테고리의 다른 글
| [고2 수학] 1학기 2차 연습 문제 (0) | 2024.06.19 |
|---|---|
| [고2 수학] 1학기 2차 지필평가 (1) | 2024.05.01 |
| [고2 수학] 1학기 1차 연습 문제 (2) | 2024.04.20 |
