삼차방정식과 사차방정식
조립제법과 근의 공식으로 푼다.
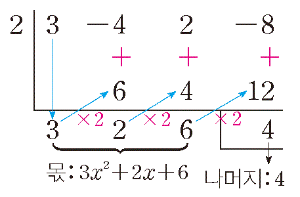

방정식 $x^3+8=0$을 풀 때, 좌변을 인수분해하면
$(x+2)(x^2-2x+4)=0$
$x+2=0$ 또는 $x^2-2x+4=0$
근의 공식으로 $x^2-2x+4=0$를 풀면
$x=\frac{-(-2)\pm\sqrt{(-2)^{2}-4(1)(4)}}{2(1)}$
따라서 주어진 방정식의 근은
$x=-2$ 또는 $x=1\pm\sqrt{3}i$
연립이차방정식
대입하여 푼다.
연립이차방정식 $\begin{cases}x^2+xy-2y^2=0\cdots㉠\\2x^2-y^2=49\cdots㉡\end{cases}$를 풀 때, ㉠의 좌변을 인수분해하면
$(x-y)(x+2y)=0$
$x=y$ 또는 $x=-2y$
(1) $x=y$를 ㉡에 대입하면
$2y^2-y^2=49$, $y^2=49$, 즉 $y=\pm7$
$y=7$일 때 $x=7$, $y=-7$일 때 $x=-7$
(2) $x=-2y$를 ㉡에 대입하면
$8y^2-y^2=49$, $y^2=7$, 즉 $y=\pm\sqrt{7}$
$y=\sqrt{7}$일 때 $x=-2\sqrt{7}$, $y=-\sqrt{7}$일 때 $x=2\sqrt{7}$
(1), (2)에서 구하는 해는 $\begin{cases}x=7\\y=7\end{cases}$ 또는 $\begin{cases}x=-7\\y=-7\end{cases}$ 또는 $\begin{cases}x=-2\sqrt{7}\\y=\sqrt{7}\end{cases}$ 또는 $\begin{cases}x=2\sqrt{7}\\y=-\sqrt{7}\end{cases}$
연립일차부등식

연립일차부등식 $5x-3<2x+3<4x+5$를 풀 때,
$\begin{cases}5x-3<2x+3\cdots㉠\\2x+3<4x+5\cdots㉡\end{cases}$
부등식 ㉠을 풀면 $3x<6$, 즉 $x<2$
부등식 ㉡을 풀면 $-2x<2$, 즉 $x>-1$
따라서 구하는 해는 $-1<x<2$
이차부등식과 연립이차부등식
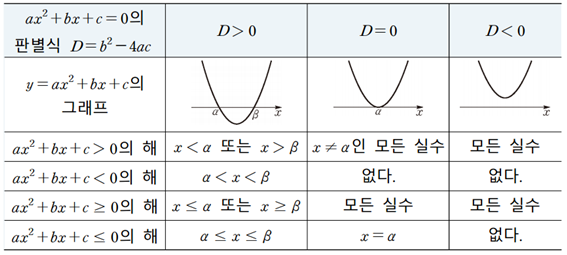
이차부등식 $x^2-5x+6<0$을 풀 때,
$(x-2)(x-3)$이고,
$D=(-5)^2-4(1)(6)$, $D>0$
따라서 구하는 해는 $2<x<3$ 이다.
두 점 사이의 거리
$\overline{AB}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$
두 점 $A(1,3)$, $B(3, -1)$ 사이의 거리는
$\sqrt{(3-1)^2+(-1-3)^2}=2\sqrt{5}$
선분의 내분과 외분

두 점 $A(1, -3)$, $B(4, 3)$을 이은 선분 $AB$를 $1:2$로 외분하는 점 $Q$의 좌표를 $(x, y)$라 하면
$x=\frac{1\times4-2\times1}{1-2}=-2$
$y=\frac{1\times3-2\times(-3)}{1-2}=-9$
$Q(-2, -9)$
직선의 방정식
한 점과 기울기가 주어진 직선의 방정식
좌표평면 위의 점 $A(x_1, y_1)$을 지나고 기울기가 $m$인 직선의 방정식은
$y-y_1=m(x-x_1)$
두 점을 지나는 직선의 방정식
좌표평면 위의 서로 다른 두 점 $A(x_1, y_1), B(x_2, y_2)$를 지나는 직선의 방정식은
(1) ${x_1}\neq{x_2}$일 때 $y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1)$
(2) $x_1=x_2$일 때 $x=x_1$
다음 두 점 $(2, -1)$, $(3, 2)$을 지나는 직선의 방정식을 구할 때,
$y-(-1)=\frac{2-(-1)}{3-2}(x-2)$
$y+1=3x-6$
$y=3x-7$
두 직선의 평행과 수직
두 직선의 평행 조건
두 직선 $y=mx+n$과 $y=m'x+n'$에서
(1) 두 직선이 서로 평행하면 $m=m'$, $n\neq{n'}$이다.
(2) $m=m'$, $n\neq{n'}$이면 두 직선은 서로 평행하다.
두 직선의 수직 조건
두 직선 $y=mx+n$과 $y=m'x+n'$에서
(1) 두 직선이 서로 수직이면 $mm'=-1$이다.
(2) $mm'=-1$이면 두 직선은 서로 수직이다.
점 $(2,4)$를 지나고 직선 $y=2x+1$에 수직인 직선의 방정식을 구할 때,
구하는 직선의 기울기를 $m$이라 하면
직선 $y=2x+1$의 기울기가 $2$이므로 $2m=-1$에서
$m=-\frac{1}{2}$
따라서 직선의 방정식은
$y-4=-\frac{1}{2}(x-2)$
즉 $y=-\frac{1}{2}x+5$
점과 직선 사이의 거리
점 $(x_1,y_1)$과 직선 $ax_1+by_1+c=0$ 사이의 거리 $d$는
$d=\frac{|ax_1+by_1+c|}{\sqrt{a^2+b^2}}$
점 $(3,-2)$와 직선 $3x+4y+2=0$ 사이의 거리는
$\frac{|3\times3+4\times(-2)+2|}{\sqrt{3^2+4^2}}=\frac{3}{5}$
원의 방정식
중심이 $(a,b)$이고 반지름의 길이가 $r$인 원의 방정식은
$(x-a)^2+(y-b)^2=r^2$
$x^2+y^2+4x-4y-4=0$은
$(x+2)^2+(y-2)^2=12$이므로
중심이 $(-2,2)$이고 반지름의 길이가 $2\sqrt{3}$인 원이다.
'고1 > 수학' 카테고리의 다른 글
| [고1 수학] 2학기 2차 지필평가 (0) | 2023.12.08 |
|---|---|
| [고1 수학] 2학기 1차 지필평가 (2) | 2023.09.17 |
| [고1 수학] 1학기 1차 지필평가 (0) | 2023.07.12 |
